What is N?

Problem's Link:

Mean:

给你三个数b、P、M，让你求有多少个n满足下式。

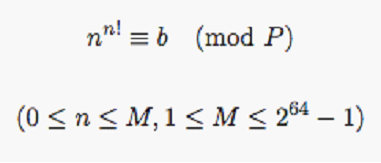
analyse:

看到数据被吓到了，没半点思路，后来看了解题报告，方法竟然是暴力！

当然暴力是有条件的。

有这样一个公式：

A^x = A^(x % Phi(C) + Phi(C)) (mod C) （x>=Phi(C)）

这个公式的具体证明原来在aekdycoin的百度空间有，但是随着百度空间被转移(百度作死，流失了好多优质的文章==)，这篇文章的完整版也流失了。

我们就当这个公式是定理吧！

当n!<Phi(C)时，此时我们暴力解决就可。

当n!大于phi（P）的时候，就需要用上面的降幂公式了。

方法还是暴力，n!%phi(p)会出现0，这是必然的，至少n>=phi(p)为0，

那么(n+1)!%phi(p)也为0，这便出现了重复，转变为n^(phi(p))%p==b的问题了。

固定了指数，根据鸽巢原理，余数是循环的，那么只要找出p个的结果，之后通过循环节求解便可以了。

Trick:当P为1的时候，b为0，这时候答案是m+1,不过m可能为2^64-1，如果加1的话就会溢出，巨坑。

Time complexity: O(N)

Source code:

/*
* this code is made by crazyacking
* Verdict: Accepted
* Submission Date: 2015-08-25-23.41
* Time: 0MS
* Memory: 137KB
*/
#include <queue>
#include <cstdio>
#include <set>
#include <string>
#include <stack>
#include <cmath>
#include <climits>
#include <map>
#include <cstdlib>
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using
namespace
std; 
typedef
__int64( 
LL); 
typedef
unsigned
__int64( 
ULL); 
const
double
eps( 
1e-8); 
LL
get_eular( 
LL
m) 
{ 
LL
ret
=
1; 
for( 
LL
i
=
2; 
i
*
i
<=
m; 
i
++) 
if( 
m
%
i
==
0) 
{ 
ret
*=
i
-
1; 
m
/=
i; 
while( 
m
%
i
==
0) 
{ 
m
/=
i; 
ret
*=
i; 
}
}
if( 
m
>
1) 
ret
*=
m
-
1; 
return
ret; 
}
long
long
Quickpow( 
long
long
a
,
long
long b 
,
long
long
m) 
{ 
long
long
ans
=
1; 
while(b) 
{ 
if(b 
&
1) 
{ 
ans
=( 
ans
*
a) 
%
m
,b 
--; 
}
            b 
/=
2
,
a
=
a
*
a
%
m; 
}
return
ans; 
}
LL b 
,p 
,
m
,
ring
[
100010
];
int
main() 
{ 
int
t
,
Cas
=
0; 
scanf( 
"%d"
,
&
t); 
while( 
t
--) 
{ 
scanf( 
"%I64u %I64u %I64u"
,
&b 
,
&p 
,
&
m); 
if(p 
==
1) 
{ 
if( 
m
==
18446744073709551615ULL) 
printf( 
"18446744073709551616
\n
"); 
else
printf( 
"%I64u
\n
"
,
m
+
1); 
continue; 
}
LL
i
=
0
,
phi
=
get_eular(p 
),
fac
=
1
,
ans
=
0; 
for( 
i
=
0; 
i
<=
m
&&
fac
<=
phi; 
i
++) 
{ 
if( 
Quickpow( 
i
,
fac
,p) 
==b) 
ans
++; 
fac
*=
i
+
1; 
}
fac
=
fac
%
phi; 
for(; 
i
<=
m
&&
fac; 
i
++) 
{ 
if( 
Quickpow( 
i
,
fac
+
phi
,p) 
==b) 
ans
++; 
fac
=( 
fac
*( 
i
+
1)) 
%
phi; 
}
if( 
i
<=
m) 
{ 
LL
cnt
=
0; 
for( 
int
j
=
0; 
j
<p; 
j
++) 
{ 
ring
[
j
]
=
Quickpow( 
i
+
j
,
phi
,p); 
if( 
ring
[
j
]
==b) 
cnt
++; 
}
LL
idx
=( 
m
-
i
+
1) 
/p; 
ans
+=
cnt
*
idx; 
LL
remain
=( 
m
-
i
+
1) 
%p; 
for( 
int
j
=
0; 
j
<
remain; 
j
++) 
if( 
ring
[
j
]
==b) 
ans
++; 
}
printf( 
"Case #%d: %I64u
\n
"
,
++
Cas
,
ans); 
}
return
0; 
}
/